Hi YOU
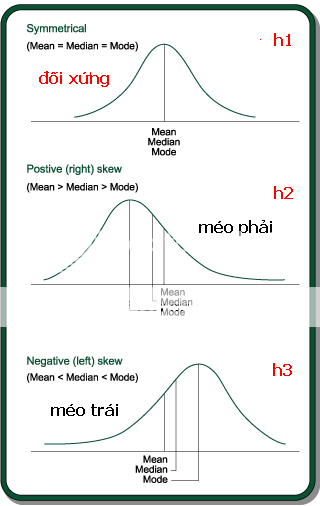
Giả thiết của lý thuyết này là return được phân bổ theo 1 Normal Distribution tuyệt đối, nghĩa là có mean và có variance (or standard deviation) và distribution curve có dạng chuông rất đối xứng.
Ý bạn? Hàm phân phối return là một hàm phân phối xác suất chuẩn (có giá trị trung bình, và độ lệch chuẩn) hay phân phối đều? Đường phân bố xác suất là đường chuông lồi đối xứng như h1 trong hình?
Phân bổ theo Normal Disitribution thì có nhưng hoặc méo trái hoặc méo phải. Sự méo (lệch) này được đo bằng skewness.
Thể hiện trong h2 và h3?
Ví dụ ta tính giá trung bình 100 ngày của 1 cổ phiếu và đạt được 1 giá trị trung bình dương = 20%. 20% lợi nhuận là tốt để đầu tư nếu chỉ dựa trên giá trị trung bình.
Không mường tượng rõ lắm ví dụ này? Hình như bạn đánh máy nhầm một chút cái câu "Ví dụ ta tính giá trung bình 100 ngày của 1 cổ phiếu và đạt được 1 giá trị trung bình dương = 20%" nên mình hơi mất thời gian chỗ này. Anyway, có phải ý bạn là "tính tỷ lệ lợi nhuận thu được của 100 cổ phiếu trong 20 ngày"? Giá trị trung bình dương 20% đó là lợi nhuận trung bình đánh giá dựa vào mean đúng ko? Mean nếu giải thích = đại số thì có lẽ mình hiểu nhưng trên hình vẽ (h1, h2, h3) bạn có thể nói rõ hơn?
Hỏi bạn chút về mấy cái hình đã! Trục tung của các hình h1, h2, h3 chính là đường tập hợp các giá trị xác suất (probability) có thể xảy ra biến cố A nào đó? Trục hoành là trục thể hiện giá trị biến cố A (theo như ví dụ của bạn thì đó là giá trị lợi nhuận thể hiện ở con số %)? Đúng/Sai?
Nếu sai! Dừng luôn ở đây và giải thích giúp mình để mình hiểu đúng! (Thể hiện trên đồ thị, hình vẽ)
Nếu đúng! Cho mình hỏi tiếp phần "skewness"
20% lợi nhuận là tốt để đầu tư nếu chỉ dựa trên giá trị trung bình. Nhưng khi lấy skewness, ta đạt được 1 skewness âm, điều này nghĩa là trên 100 ngày, đa số ngày là có return dương, nhưng bỗng nhiên có 1 hoặc 2 ngày có return âm rất mạnh. Việc có một số nhỏ return âm mạnh này không thể hiện trong mean nhưng trong skewness thì nó thể hiện = 1 giá trị âm, nghĩa là các return dương bị ảnh hưởng mạnh bởi 1 số nhỏ return âm đáng kể.
"skewness" ~ "độ lệch, độ méo": giúp ta biết được những "đột biến" không mong muốn và loại nó ra (nếu cần) trong quá trình ra quyết định đầu tư? "Skewness" khắc phục được một số thiếu sót của mean? Okie nhé?
Việc có một số nhỏ return âm mạnh này không thể hiện trong mean nhưng trong skewness thì nó thể hiện = 1 giá trị âm, nghĩa là các return dương bị ảnh hưởng mạnh bởi 1 số nhỏ return âm đáng kể.
Nhưng tớ hỏi chút về nhận diện trên hình, làm sao biết một "skewness" âm để biết trong 100 ngày thì có 1 ngày return âm (âm mạnh)?
Việc bỗng nhiên 1 số return rất âm nhảy vào như vậy là 1 điều không hay và là 1 loại rủi ro cần tránh. Nếu mua 1 cổ phiếu có skewness âm, thì nghĩa là cho dù mean return có dương thì trong tương lai vẫn dễ bị ăn return âm. Độ âm bao nhiêu tỉ lệ vào độ âm skewness.
Ngược lại, nếu mean return rất thấp nhưng skewness cao thì nghĩa là trong tương lai có khả năng ăn 1 số return cao bất ngờ; Cái này là skewness dương.
Về mặt logic thì hiểu rằng, khi "độ biến động" hay "độ lệch, độ méo" lợi nhuận (gọi là skewness ấy) mà cao hoặc rất cao (mang giá trị dương) trong khi khả năng lợi nhuận bình quân (gọi là mean đó) thấp sàn sàn thì tốt vì trường hợp cùng quẫn rủi ro nhất cũng chỉ đạt lợi nhuận = giá trị mean hoặc thấp hơn tí NHƯNG ko có giá trị lợi nhuận âm.
Còn nếu skewness âm thì "đi
đêm mãi cũng có
ngày gặp ma" dù mean dương? Đúng rồi!
Nhưng mình không hiểu trên hình? Và cách tích/công thức tính skew và mean? (Có thể mình chưa đọc tới đoạn đó hoặc đọc chưa kỹ!) Có gì (nếu bạn rảnh) giải thích tiếp đoạn này giúp mình! Thanks!
---------------chuyển sang phần kurtosis-------------------------------
Skewness là moment bậc 3.
Kurtosis là moment bậc 4.
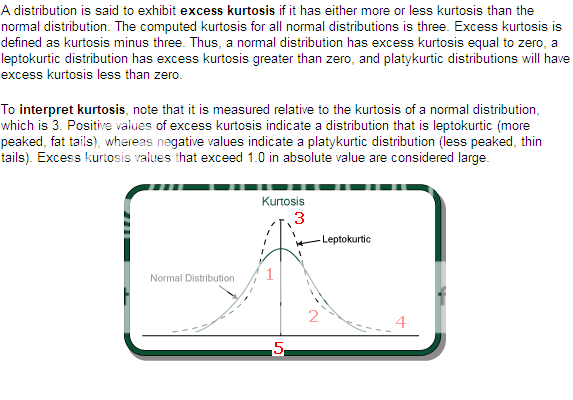
Mean return thường được tính để làm benchmark so sánh giữa các cổ phiếu. Nếu kurtosis thấp thì nghĩa là các giá trị không có xu hướng đi xa khỏi mean return, như vậy độ an toàn và thanh khoản cao. Cái này gọi là leptokurtic, đường Normal curve rất hẹp, nên leptokurtic nghĩa là "lép".
OK, nhưng giải thích các vị trí trên hình giúp mình! Mình gọi tên các vị trí để bạn gọi tên trong quá trình giải thích rồi! Nói rõ lại trên hình giúp mình nhé!
Dao động ít thì rủi ro ít. Trong 1 thị trường, những cổ phiếu rủi ro ít nhất (dao động ít nhất) có nhiều khả năng được gọi là blue-chips.
Chưa chắc! Lúc rảnh sẽ thống kê chuyện này! Nhất là ở HOSTC và HASTC!
Càng leptokurtic càng tốt.
"Lép" quá sợ có mất tính thanh khoản không?
Ngược lại, platokurtic nghĩa là dao động mạnh, có thể rất cao về bên dương so với mean return, cũng có thể rất thấp về bên âm so với mean return. Dao động mạnh thì rủi ro nhiều, thanh khoản sẽ thấp vì không an toàn.
Một loạt blue chip VN như SSI, FPT, STB, ACB dao động cực mạnh, rủi ro rất nhiều nhưng thanh khoản cực cao? (trừ thời điểm bây giờ).
Mình ko nghĩ tính thanh khoản lại có liên quan đến mean và skew, hay "lép" ở đây!
Ở đây chỉ nói rủi ro thôi!
Trong phân tích đầu tư, skewness và kurtosis là 2 chỉ số cần phải đo ngay sau mean return và variance return vì đây mới thực sự là những chỉ số đo rủi ro. Điều này ít người biết. Lí tưởng là 1 cổ phiếu có skewness dương và kurtosis nhỏ (leptokurtic) vì như vậy có nhiều khả năng bất thình lình ăn to (skewness dương) mà độ an toàn lại cao (kurtosis thấp).
Yes!
Túm lại, mấy chỗ chưa rõ làm rõ giúp mình nhé! Theo hình vẽ thì giải thích luôn giúp mình ý nghĩa cái "excess kurtosis"!
Thanks alot!